Overview

Getting started

We first sketch the dynamic system we want to simulate as a block diagram, for example this simple first-order system

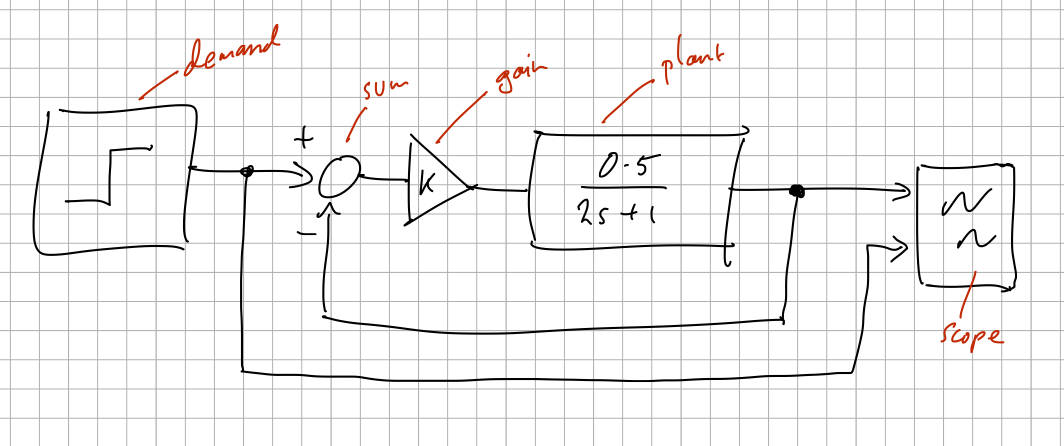
which we can express concisely with bdsim as (see bdsim/examples/eg1.py)

import bdsim

sim = bdsim.BDSim()  # create simulator
bd = sim.blockdiagram()  # create an empty block diagram

# define the blocks
demand = bd.STEP(T=1, name='demand')
sum = bd.SUM('+-')
gain = bd.GAIN(10)
plant = bd.LTI_SISO(0.5, [2, 1], name='plant')
scope = bd.SCOPE(styles=['k', 'r--'], movie='eg1.mp4')

# connect the blocks
bd.connect(demand, sum[0], scope[1])
bd.connect(sum, gain)
bd.connect(gain, plant)
bd.connect(plant, sum[1], scope[0])

bd.compile()   # check the diagram
bd.report()    # list all blocks and wires

out = sim.run(bd, 5)  # simulate for 5s

print(out)

# sim.savefig(scope, 'scope0') # save scope figure as scope0.pdf
sim.done(bd, block=True)  # keep figures open on screen

which is just 16 lines of executable code.

The red block annotations on the hand-drawn diagram are used as the names of the variables holding references to the block instance. The blocks can also have user-assigned names, see lines 8 and 11, which are used in diagnostics and as labels in plots.

After the blocks are created their input and output ports need to be connected. In bdsim all wires are point to point, a one-to-many connection is implemented by many wires, for example:

bd.connect(source, dest1, dest2, ...)

creates individual wires from source -> dest1, source -> dest2 and so on. Ports are designated using Python indexing notation, for example block[2] is port 2 (the third port) of block. Whether it is an input or output port depends on context. In the example above an index on the first argument refers to an output port, while on the second (or subsequent) arguments it refers to an input port. If a block has only a single input or output port then no index is required, 0 is assumed.

A group of ports can be denoted using slice notation, for example:

bd.connect(source[2:5], dest[3:6)

will connect source[2] -> dest[3], source[3] -> dest[4], source[4] -> dest[5]. The number of wires in each slice must be consistent. You could even do a cross over by connecting source[2:5] to dest[6:3:-1].

Line 20 assembles all the blocks and wires, instantiates subsystems, checks connectivity to create a flat wire list, and then builds the dataflow execution plan.

Line 21 generates a report, in tabular form, showing a summary of the block diagram:

Blocks::

┌───┬─────────┬─────┬──────┬────────┬─────────┬───────┐
│id │    name │ nin │ nout │ nstate │ ndstate │ type  │
├───┼─────────┼─────┼──────┼────────┼─────────┼───────┤
│ 0 │  demand │   0 │    1 │      0 │       0 │ step  │
│ 1 │   sum.0 │   2 │    1 │      0 │       0 │ sum   │
│ 2 │  gain.0 │   1 │    1 │      0 │       0 │ gain  │
│ 3 │   plant │   1 │    1 │      1 │       0 │ LTI   │
│ 4 │ scope.0 │   2 │    0 │      0 │       0 │ scope │
└───┴─────────┴─────┴──────┴────────┴─────────┴───────┘

Wires::

┌───┬──────┬──────┬──────────────────────────┬─────────┐
│id │ from │  to  │       description        │  type   │
├───┼──────┼──────┼──────────────────────────┼─────────┤
│ 0 │ 0[0] │ 1[0] │ demand[0] --> sum.0[0]   │ int     │
│ 1 │ 0[0] │ 4[1] │ demand[0] --> scope.0[1] │ int     │
│ 2 │ 3[0] │ 1[1] │ plant[0] --> sum.0[1]    │ float64 │
│ 3 │ 1[0] │ 2[0] │ sum.0[0] --> gain.0[0]   │ float64 │
│ 4 │ 2[0] │ 3[0] │ gain.0[0] --> plant[0]   │ float64 │
│ 5 │ 3[0] │ 4[0] │ plant[0] --> scope.0[0]  │ float64 │
└───┴──────┴──────┴──────────────────────────┴─────────┘

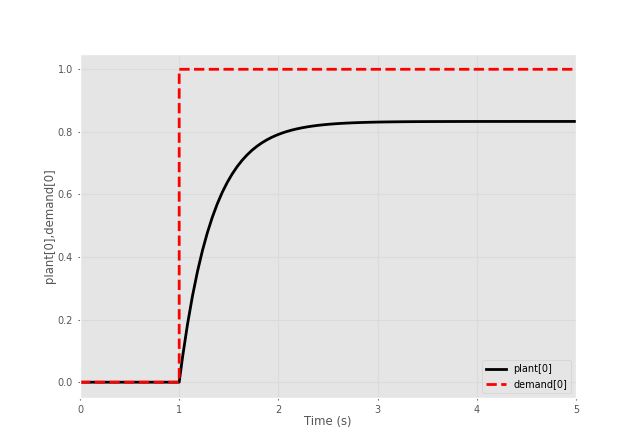
The simulation results are returned in a simple container object:

>>> out
results:
t           | ndarray (67,)
x           | ndarray (67, 1)
xnames      | list

where

t the time vector: ndarray, shape=(M,)
x is the state vector: ndarray, shape=(M,N), one row per timestep
xnames is a list of the names of the states corresponding to columns of x, eg. “plant.x0”

To record additional simulation variables we “watch” them. This can be specified by wiring the signal to a WATCH block, or more conveniently by an additional option to run:

out = sim.run(bd, 5, watch=[plant,demand])  # simulate for 5s

and now the result out has additional elements:

>>> out
results:
t           | ndarray (67,)
x           | ndarray (67, 1)
xnames      | list
y0          | ndarray (67,)
y1          | ndarray (67,)
ynames      | list

where

y0 is the time history of the first watched signal
y1 is the time history of the second watched signal
ynames is a list of the names of the states corresponding to columns of x, eg. “plant[0]”

Line 27 saves the content of the scope to be saved in the file called scope0.pdf.

Line 28 blocks the script until all figure windows are closed, or the script is killed with SIGINT.

Line 29 saves the scope graphics as a PDF file.

Line 30 blocks until the last figure is dismissed.

A list of available blocks can be obtained by:

>>> sim.blocks()
   73  blocks loaded
   bdsim.blocks.functions..................: Sum Prod Gain Clip Function Interpolate
   bdsim.blocks.sources....................: Constant Time WaveForm Piecewise Step Ramp
   bdsim.blocks.sinks......................: Print Stop Null Watch
   bdsim.blocks.transfers..................: Integrator PoseIntegrator LTI_SS LTI_SISO
   bdsim.blocks.discrete...................: ZOH DIntegrator DPoseIntegrator
   bdsim.blocks.linalg.....................: Inverse Transpose Norm Flatten Slice2 Slice1 Det Cond
   bdsim.blocks.displays...................: Scope ScopeXY ScopeXY1
   bdsim.blocks.connections................: Item Dict Mux DeMux Index SubSystem InPort OutPort
   roboticstoolbox.blocks.arm..............: FKine IKine Jacobian Tr2Delta Delta2Tr Point2Tr TR2T FDyn IDyn Gravload
   ........................................: Inertia Inertia_X FDyn_X ArmPlot Traj JTraj LSPB CTraj CirclePath
   roboticstoolbox.blocks.mobile...........: Bicycle Unicycle DiffSteer VehiclePlot
   roboticstoolbox.blocks.uav..............: MultiRotor MultiRotorMixer MultiRotorPlot
   machinevisiontoolbox.blocks.camera......: Camera Visjac_p EstPose_p ImagePlane

More details can be found at:

Using operator overloading

Wiring, and some simple arithmetic blocks like GAIN, SUM and PROD can be implicitly generated by overloaded Python operators. This strikes a nice balance between block diagram coding and Pythonic programming.

import bdsim

sim = bdsim.BDSim()  # create simulator
bd = sim.blockdiagram()  # create an empty block diagram

# define the blocks
demand = bd.STEP(T=1, name='demand')
plant = bd.LTI_SISO(0.5, [2, 1], name='plant')
scope = bd.SCOPE(styles=['k', 'r--'], movie='eg1.mp4')

# connect the blocks
scope[0] = plant
scope[1] = demand
plant[0] = 10 * (demand - plant)

bd.compile()   # check the diagram
bd.report()    # list all blocks and wires

out = sim.run(bd, 5)  # simulate for 5s
# out = sim.run(bd, 5 watch=[plant,demand])  # simulate for 5s
print(out)

# sim.savefig(scope, 'scope0') # save scope figure as scope0.pdf
sim.done(bd, block=True)  # keep figures open on screen

This requires fewer lines of code and the code is more readable. Importantly, it results in in exactly the same block diagram in terms of blocks and wires:

┌───┬──────┬──────┬──────────────────────────────┬─────────┐
│id │ from │  to  │         description          │  type   │
├───┼──────┼──────┼──────────────────────────────┼─────────┤
│ 0 │ 1[0] │ 2[0] │ plant[0] --> scope.0[0]      │ float64 │
│ 1 │ 0[0] │ 2[1] │ demand[0] --> scope.0[1]     │ int     │
│ 2 │ 0[0] │ 3[0] │ demand[0] --> _sum.0[0]      │ int     │
│ 3 │ 1[0] │ 3[1] │ plant[0] --> _sum.0[1]       │ float64 │
│ 4 │ 3[0] │ 4[0] │ _sum.0[0] --> _gain.0(10)[0] │ float64 │
│ 5 │ 4[0] │ 1[0] │ _gain.0(10)[0] --> plant[0]  │ float64 │
└───┴──────┴──────┴──────────────────────────────┴─────────┘

The implicitly created blocks have names prefixed with an underscore.