Catadioptric camera

Model the geometry of a catadioptric camera.

class machinevisiontoolbox.Camera.CatadioptricCamera(k=None, projection='equiangular', maxangle=None, **kwargs)[source]
Inheritance diagram of machinevisiontoolbox.Camera.CatadioptricCamera

Create catadioptric camera projection model

Parameters

  • k (float, optional) – scale factor

  • projection (str, optional) – projection model: 'equiangular' [default], 'sine', 'equisolid' or 'stereographic'

  • kwargs – arguments passed to CameraBase constructor

A catadioptric camera comprises a perspective camera pointed at a convex mirror, typically paraboloidal or conical.

The elevation angle range is from \(-\pi/2\) (below the mirror) to maxangle above the horizontal plane. The mapping from elevation angle \(\theta\) to image plane radius is given by:

Projection

\(r(\theta)\)

equiangular

\(r = k \theta\)

sine

\(r = k \sin \theta\)

equisolid

\(r = k \sin \frac{\theta}{2}\)

stereographic

\(r = k \tan \frac{\theta}{2}\)

Note

  • If K is not specified it is computed such that the circular imaging region maximally fills the image plane.

  • This camera model assumes central projection, that is, the focal point is at z=0 and the image plane is at z=f. The image is not inverted.

References

  • Robotics, Vision & Control for Python, Section 13.3.2, P. Corke, Springer 2023.

Seealso

CameraBase CentralCamera FishEyeCamera SphericalCamera

property camtype

Set/get camera type (base method)

A camera has a string-valued type that can be read and written. This is unique to the camera subclass and projection model.

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera();
>>> camera.camtype
'perspective'
>>> camera.camtype = "foo"
>>> camera.camtype
'foo'
clf()

Clear the virtual image plane (base method)

Every camera object has a virtual image plane drawn using Matplotlib. Remove all points and lines from the image plane.

Seealso

plot_point plot_line disp

disp(im, **kwargs)

Display image on virtual image plane (base method)

Parameters

  • im (Image instance) – image to display

  • kwargs – options to idisp

An image is displayed on camera’s the virtual image plane.

Seealso

machinevisiontoolbox.base.idisp

property height

Get image plane height (base method)

Returns

height

Return type

int

Image plane width, number of pixels in the u-direction

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.height
1000
Seealso

nv width

property imagesize

Set/get size of virtual image plane (base method)

The dimensions of the virtual image plane is a 2-tuple, width and height, that can be read or written. For writing the size must be an iterable of length 2.

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.imagesize
array([1000, 1000])
>>> camera.imagesize = (500, 500)
>>> camera.imagesize
array([500, 500])

Note

If the principal point is not set, then setting imagesize sets the principal point to the centre of the image plane.

Seealso

width height nu nv

move(T, name=None, relative=False)

Move camera (base method)

Parameters

  • T (SE3) – pose of camera frame

  • relative (bool, optional) – move relative to pose of original camera, defaults to False

Returns

new camera object

Return type

CameraBase subclass

Returns a copy of the camera object with pose set to T.

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> from spatialmath import SE3
>>> camera = CentralCamera();
>>> camera.move(SE3.Trans(0.1, 0.2, 0.3))
           Name: perspective-moved [CentralCamera]
     pixel size: 1.0 x 1.0
           pose: t = 0.1, 0.2, 0.3; rpy/yxz = 0°, 0°, 0°
   principal pt: [0. 0.]
   focal length: [1. 1.]

>>> camera
           Name: perspective [CentralCamera]
     pixel size: 1.0 x 1.0
           pose: t = 0, 0, 0; rpy/yxz = 0°, 0°, 0°
   principal pt: [0. 0.]
   focal length: [1. 1.]

Note

The plot method of this cloned camera will create a new window.

Seealso

pose

property name

Set/get camera name (base method)

A camera has a string-valued name that can be read and written.

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera();
>>> camera.name
'perspective'
>>> camera.name = "foo"
>>> camera.name
'foo'
property noise

Set/Get projection noise (base method)

Returns

standard deviation of noise added to projected image plane points

Return type

float

The noise parameter is set by the object constructor.

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.project_point([0, 0, 3])
array([[500.],
       [500.]])
>>> camera.noise = 2
>>> camera.project_point([0, 0, 2])
array([[501.1023],
       [498.7353]])
>>> camera.project_point([0, 0, 2])
array([[500.7471],
       [498.3055]])
Seealso

project

property nu

Get image plane width (base method)

Returns

width

Return type

int

Number of pixels in the u-direction (width)

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.nu
1000
Seealso

nv width imagesize

property nv

Get image plane height (base method)

Returns

height

Return type

int

Number of pixels in the v-direction (height)

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.nv
1000
Seealso

nu height imagesize

plot(pose=None, scale=1, shape='camera', label=True, alpha=1, solid=False, color='r', projection='ortho', frame=False, ax=None)

Plot 3D camera icon in world view (base method)

Parameters

  • pose (SE3) – camera pose

  • scale (float) – scale factor, defaults to 1

  • shape (str, optional) – icon shape: ‘frustum’ [default], ‘camera’

  • label (bool, optional) – show camera name, defaults to True

  • alpha (float, optional) – transparency of icon, defaults to 1

  • solid (bool, optional) – icon comprises solid faces, defaults to False

  • color (str, optional) – icon color, defaults to ‘r’

  • projection (str, optional) – projection model for new axes, defaults to ‘ortho’

  • ax (Axes3D, optional) – axes to draw in, defaults to current 3D axes

Returns

axes drawn into

Return type

Axes3D

Plot a 3D icon representing the pose of a camera into a 3D Matplotlib plot. Two icons are supported: the traditional frustum, and a simplistic camera comprising a box and cylinder.

Note

If pose is not given it defaults to the pose of the instance.

plot_line2(l, *args, **kwargs)

Plot 2D line on virtual image plane (base method)

Parameters

  • l (array_like(3)) – homogeneous line

  • kwargs – arguments passed to plot

Plot the homogeneous line on the camera’s virtual image plane. The line is expressed in the form

\[\ell_0 u + \ell_1 v + \ell_2 = 0\]

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default()
>>> camera.plot_line2([1, 0.2, -500])

Note

  • Successive calls add items to the virtual image plane.

  • This method is common to all CameraBase subclasses, but it invokes a camera-specific projection method.

Seealso

plot_point plot_line3 clf

plot_point(P, *fmt, return_artist=False, objpose=None, pose=None, ax=None, **kwargs)

Plot points on virtual image plane (base method)

Parameters

  • P (ndarray(3,), ndarray(3,N), or ndarray(2,), ndarray(2,N)) – 3D world point or points, or 2D image plane point or points

  • objpose (SE3, optional) – transformation for the 3D points, defaults to None

  • pose (SE3, optional) – pose of the camera, defaults to None

  • ax (matplotlib.axes) – axes to plot into

  • kwargs – additional arguments passed to plot

Returns

Matplotlib line objects

Return type

list of Line2d

3D world points are first projected to the image plane and then plotted on the camera’s virtual image plane. Points are organized as columns of the arrays.

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default()
>>> camera.plot_point([0.2, 0.3, 2])
>>> camera.plot_point([0.2, 0.3, 2], 'r*')
>>> camera.plot_point([0.2, 0.3, 2], pose=SE3(0.1, 0, 0))

(Source code)

Note

  • Successive calls add items to the virtual image plane.

  • This method is common to all CameraBase subclasses, but it invokes a camera-specific projection method.

Seealso

plot_line2 plot_line3 plot_wireframe clf

plot_wireframe(X, Y, Z, *fmt, objpose=None, pose=None, nsteps=21, **kwargs)

Plot 3D wireframe in virtual image plane (base method)

Parameters

  • X (ndarray(N,M)) – world X coordinates

  • Y (ndarray(N,M)) – world Y coordinates

  • Z (ndarray(N,M)) – world Z coordinates

  • objpose (SE3, optional) – transformation for the wireframe points, defaults to None

  • pose (SE3, optional) – pose of the camera, defaults to None

  • nsteps (int, optional) – number of points for each wireframe segment, defaults to 21

  • kwargs – arguments passed to plot

The 3D wireframe is projected to the camera’s virtual image plane. Each wire link in the wireframe is approximated by nsteps points, each of which is projected, allowing straight edges to appear curved.

Example:

>>> from machinevisiontoolbox import CentralCamera, mkcube
>>> from spatialmath import SE3
>>> camera = CentralCamera.Default()
>>> X, Y, Z = mkcube(0.2, pose=SE3(0, 0, 1), edge=True)
>>> camera.plot_wireframe(X, Y, Z, 'k--')

(Source code, png, hires.png, pdf)

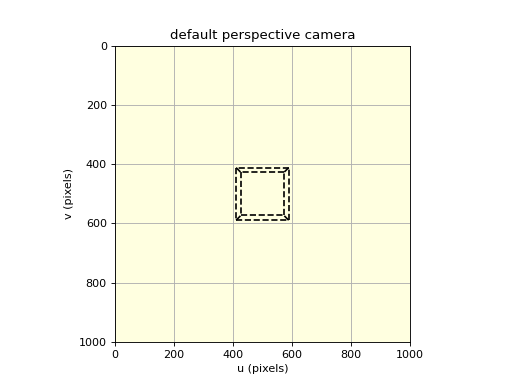
_images/camera-catadiop-2.png
Seealso

mkcube spatialmath.base.cylinder spatialmath.base.sphere spatialmath.base.cuboid

property pose

Set/get camera pose (base method)

The camera pose with respect to the global frame can be read or written as an SE3 instance.

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> from spatialmath import SE3
>>> camera = CentralCamera();
>>> camera.pose
SE3(array([[1., 0., 0., 0.],
           [0., 1., 0., 0.],
           [0., 0., 1., 0.],
           [0., 0., 0., 1.]]))
>>> camera.pose = SE3.Trans(1, 2, 3)
>>> camera
           Name: perspective [CentralCamera]
     pixel size: 1.0 x 1.0
           pose: t = 1, 2, 3; rpy/yxz = 0°, 0°, 0°
   principal pt: [0. 0.]
   focal length: [1. 1.]

Note

Changes the pose of the current camera instance, whereas move clones the camera instance with a new pose.

Seealso

move

property pp

Set/get principal point coordinate (base method)

The principal point is the coordinate of the point where the optical axis pierces the image plane. It is a 2-tuple which can be read or written. For writing the size must be an iterable of length 2.

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.pp
array([500., 500.])
Seealso

u0 v0

reset()

Reset camera pose (base method)

Restore camera to a copy of the pose given to the constructor. The copy means that the camera pose can be modified freely, without destroying the initial pose value.

property rho

Get pixel dimensions (base method)

Returns

horizontal pixel size

Return type

ndarray(2)

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera();
>>> camera.rhov
1.0
Seealso

rhou rhov

property rhou

Get pixel width (base method)

Returns

horizontal pixel size

Return type

float

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.rhou
1e-05
Seealso

rhov rho

property rhov

Get pixel width (base method)

Returns

vertical pixel size

Return type

float

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.rhov
1e-05
Seealso

rhov rho

property u0

Get principal point: horizontal coordinate (base method)

Returns

horizontal component of principal point

Return type

float

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera();
>>> camera.u0
0.0
Seealso

v0 pp

property v0

Get principal point: vertical coordinate (base method)

Returns

vertical component of principal point

Return type

float

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera();
>>> camera.v0
0.0
Seealso

u0 pp

property width

Get image plane width (base method)

Returns

width

Return type

int

Image plane height, number of pixels in the v-direction

Example:

>>> from machinevisiontoolbox import CentralCamera
>>> camera = CentralCamera.Default();
>>> camera.width
1000
Seealso

nu height

project_point(P, pose=None, objpose=None)[source]

Project 3D points to image plane

Parameters

  • P (array_like(3), array_like(3,n)) – 3D world point or points

  • pose (SE3, optional) – camera pose with respect to the world frame, defaults to camera’s pose attribute

  • objpose (SE3, optional) – 3D point reference frame, defaults to world frame

  • visibility (bool) – test if points are visible, default False

Raises

ValueError – [description]

Returns

image plane points

Return type

ndarray(2,n)

Project world points to the catadioptric camera image plane.

World points are given as a 1D array or the columns of a 2D array of Euclidean coordinates. The computed image plane coordinates are Euclidean and given as a 1D array or the corresponding columns of a 2D array.

If pose is specified it is used for the camera pose instead of the attribute pose. The object’s attribute is not updated.

The points P are by default with respect to the world frame, but they can be transformed by specifying objpose.

Seealso

plot_point